La ecuación logística discreta ^{8A diferencia de la ecuación logística continua, en la ecuación logística discreta los procesos estudiados se observan en instantes puntuales distintos y los datos experimentales obtenidos de esta manera forman entonces un conjunto discreto y ordenado de valores. Para el modelo que tomamos para este trabajo son la cantidad de población tras el primer ciclo, el siguiente número tras el segundo ciclo, luego el tercer número, y así sucesivamente.}

Continuando con el ejemplo del crecimiento de la población, tratamos de afinar el modelo siguiendo las mismas ideas que nos condujeron al modelo logístico continuo del punto anterior. Entonces, la forma que adquiere el modelo logístico discreto es el siguiente:

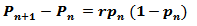
En este caso el crecimiento de la población se expresa como la fracción de la población máxima admisible existente, en el paso del periodo n al periodo n+1, dado por la diferencia P_n+1 - P_n , resultando ésta proporcional a la población existente al principio del periodo temporal y a la diferencia entre el valor de saturación y dicha población.

En la ecuación (4) y la gráfica (2) podemos observar que, dada una condición inicial P_O, queda determinada una sucesión de valores P₁,P₂ ,...,P_n . Pero en el caso discreto –a diferencia del modelo continuo en el que se puede hallar la población como función explícita del tiempo t–, es posible obtener p como función explícita de n, esto significa que no se puede resolver analíticamente la ecuación en diferencias (5), de modo que si queremos obtener al valor de P_n tendremos que calcularlo uno a uno.

Se puede transformar la ecuación (5) en otra más fácil de manejar de la siguiente manera:



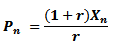
Así, obtenemos:



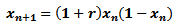
si K = 1 + r , entonces tenemos que:

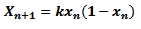
⁸ A diferencia de la ecuación logística continua, en la ecuación logística discreta los procesos estudiados se observan en instantes puntuales distintos y los datos experimentales obtenidos de esta manera forman entonces un conjunto discreto y ordenado de valores. Para el modelo que tomamos para este trabajo son la cantidad de población tras el primer ciclo, el siguiente número tras el segundo ciclo, luego el tercer número, y así sucesivamente.