mayo-agosto de 2011
plan quinquenal de desarrollo Dependencia e inequidad
tributaria de los gobiernos
estatales La explotación intensiva
y extensiva de la naturaleza Eugenio Varga, el Polonio
de la Komintern y de Stalin -Reseña -
Las regiones en México
y sus estudios -Reseña-
Nuevas causas
de la migración en México Nuevas publicaciones
Ideas sobre su posible modelación matemática
El modelo de crecimiento de la población de Verhulst
La ecuación fue propuesta por Verhulst para modelar el crecimiento de cualquier población, ya sea humana o de animales. Es una ecuación paradigmática 4Se dice que una ecuación es paradigmática cuando fue propuesta para modelar un problema o fenómeno específico, pero con el tiempo se descubre que esa ecuación sirve para ilustrar o modelar fenómenos distintos del original. En este caso la estamos usando para ilustrar el incremento de la explotación intensiva y extensiva de la naturaleza por parte del hombre. Sary Levy Carciente (2002: 14), entre otros, afirma que "Muchas de las aplicaciones de la dinámica de caos a problemas económicos son adaptaciones de la ecuación logística."
porque a pesar de su sencillez es una ecuación dinámica no lineal 5Es dinámica porque es una ecuación que nos representa la evolución de la variable en el tiempo y es no lineal porque es de segundo grado y su gráfica nos muestra claramente que su solución, en las diferentes condiciones iniciales, es una curva.
con mucho potencial para modelar y además es muy didáctica para representar un sistema dinámico no lineal que evoluciona en el tiempo.
Sean:
t = Tiempo (variable independiente).
P = Población 6Como lo explicamos en el pie de página 4, originalmente la ecuación logística de Verhulst se propuso para modelar poblaciones humanas. Pero como lo explica Levy, con ciertas adaptaciones se han hecho aplicaciones a problemas económicos. (variable dependiente).
r = Coeficiente de la razón de crecimiento de la población (parámetro).
K = Capacidad de carga 7En el modelo original, Verhulst llama capacidad de carga a los límites territoriales y de recursos que tienen las poblaciones para poder seguir creciendo. En el fenómeno que estamos ilustrando significaría el límite que tiene la naturaleza para resistir la explotación intensiva y extensiva por parte del hombre. del sistema.
Entonces,
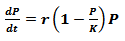
La ecuación (3) tiene la siguiente solución analítica para un problema de valor inicial:
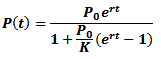
4 Se dice que una ecuación es paradigmática cuando fue propuesta para modelar un problema o fenómeno específico, pero con el tiempo se descubre que esa ecuación sirve para ilustrar o modelar fenómenos distintos del original. En este caso la estamos usando para ilustrar el incremento de la explotación intensiva y extensiva de la naturaleza por parte del hombre. Sary Levy Carciente (2002: 14), entre otros, afirma que "Muchas de las aplicaciones de la dinámica de caos a problemas económicos son adaptaciones de la ecuación logística."
5 Es dinámica porque es una ecuación que nos representa la evolución de la variable en el tiempo y es no lineal porque es de segundo grado y su gráfica nos muestra claramente que su solución, en las diferentes condiciones iniciales, es una curva.
6 Como lo explicamos en el pie de página 4, originalmente la ecuación logística de Verhulst se propuso para modelar poblaciones humanas. Pero como lo explica Levy, con ciertas adaptaciones se han hecho aplicaciones a problemas económicos.
7 En el modelo original, Verhulst llama capacidad de carga a los límites territoriales y de recursos que tienen las poblaciones para poder seguir creciendo. En el fenómeno que estamos ilustrando significaría el límite que tiene la naturaleza para resistir la explotación intensiva y extensiva por parte del hombre.